
This article is an excerpt from the Shortform book guide to "The Republic" by Plato. Shortform has the world's best summaries and analyses of books you should be reading.
Like this article? Sign up for a free trial here.
What’s the nature of knowledge and reality? What makes some ideas more true or valuable than others?
Plato’s analogy of the divided line explores these questions in his seminal work The Republic. This thought-provoking concept categorizes different levels of understanding, from illusions to ultimate truth. It offers insights into how we perceive the world and what constitutes genuine knowledge.
Keep reading for an exploration of Plato’s philosophy, and discover how it still influences our thinking today.
Plato’s Analogy of the Divided Line
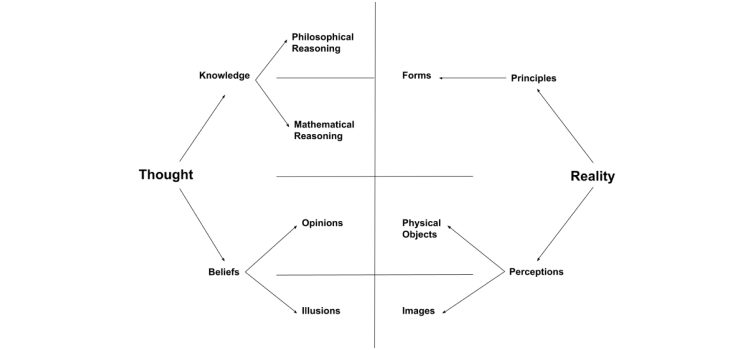
Plato’s analogy of the divided line appears as part of a dialogue that takes place in books V through VII of The Republic. In this dialogue, Plato (through the character Socrates) argues that philosophers make the best leaders, and he uses three allegories to show why. The analogy of the divided line explains why an ideal ruler needs philosophical knowledge.
According to Socrates, there’s a hierarchy of human thought—some thoughts or claims are better than others. He argues that the more provable, universal, and unchanging a thought is, the better it is because these criteria determine how certain we can be of its truth. To further illustrate this hierarchy of truth, Socrates compares thoughts to objects in the world. He categorizes them in a line divided into several sections.
Each row of the divided line represents a different category of thought. Let’s explore the hierarchy of these categories in more detail.
(Shortform note: Plato’s earlier dialogue The Symposium describes a more specific kind of “ascent” that is similar in some ways to the divided line. In a passage scholars call “the ladder of love,” he talks about how to “ascend” one’s appreciation and desire for beauty. Much like the divided line, the ladder of love ascends from the specific and concrete to the abstract and universal. Someone at the bottom of the ladder desires specific beautiful things but doesn’t necessarily know what makes them beautiful, while someone at the top understands the nature of beauty and desires it in all its forms. Keep this contrast between specific examples and broad concepts in mind as you read through the description of the divided line.)
Lowest Level: Illusions and Images
Illusions are beliefs not backed by evidence. Socrates says these are therefore the lowest form of knowledge, as very little suggests they’re true. For example, the popular idea that “sunflowers always point toward the sun” is an illusion; it’s commonly repeated and believed even though it has little to no evidence behind it. Socrates compares illusions to our perceptions of images or shadows in the world around us—you see your reflection in a mirror, but there isn’t another real copy of you behind or within it.
(Shortform note: According to Plato, art also falls into the category of illusion because it merely represents objects in the world like a reflection or shadow. However, Plato’s relationship toward art and poetry in particular is complex; on the one hand, he often discusses the dangerous moral influence of art. On the other hand, Plato’s own works are dramatic and often use allegories, myths, and other artistic or poetic devices. Some scholars suggest Plato does so to paraphrase and simplify his more complex points. Or, to use the language of the divided line, he offers illusions as a shorthand for concepts he understands on a deeper level.)
Second Level: Opinions and Objects
Opinions are beliefs backed by evidence. They’re therefore superior to illusions but still don’t provide concrete knowledge. For example, there’s plenty of evidence that gravity exists, but we can’t be certain it does or that it always will. Socrates compares opinions to our perceptions of physical objects. We can see and touch a table to see if it’s there, but those perceptions are still founded on assumptions—that we know what a table is, that our faculties are working correctly, and so on.
| Opinions, Objects, and the Limits of Perception Plato describes the first two levels of the divided line in terms of sense perceptions—illusions are false perceptions, while opinions backed by evidence and perceptions of objects are generally reliable. However, he still believes perceptions are inherently limited, which is why they make up the lower half of the line. To further understand why, we can turn to 18th-century Scottish philosopher David Hume. Hume famously argued that there’s no rational foundation for knowledge. In other words, he believed nothing was definitively provable because all human knowledge and reasoning rested on unreliable empirical evidence. For example, imagine you hold up a pencil and then drop it. You would expect it to fall and would most likely be correct. However, there’s no way of definitively knowing the pencil will fall before you drop it. You can drop thousands of pencils and gain overwhelming empirical evidence that pencils fall when dropped, but evidence alone won’t prove that pencils always fall when dropped. This is why something like gravity—typically accepted by modern society as a fact—still counts as an opinion according to Plato’s theory. Hume argues that all forms of thought ultimately rely on empirical evidence, as even logic like two plus two equals four relies on our perceptions of cause and effect. On the other hand, Plato believes there are types of thought that are independent of empirical evidence and its limitations—types of thought that are therefore higher on the divided line than opinions and objects. |
Third Level: Knowledge and the Forms
Knowledge is provably universally true and unchanging. Socrates explains that we can arrive at knowledge through mathematical and philosophical reasoning. For example, we can use mathematical reasoning to prove that two plus two always equals four and will never stop equalling four. Therefore, we know that two plus two equals four. Similarly, Socrates suggests that philosophical reasoning and debate can provide provable, universal, and unchanging definitions of concepts like justice and beauty.
Socrates explains that knowledge is to thought as forms are to reality. The forms, he explains, are unchanging, universal, perfect versions of objects and concepts that exist in a separate realm. Objects imitate or derive from these forms in the same way that images derive from objects. For example, we understand what a perfect circle is in theory, but all existing circles in the world have flaws, however minuscule, that make them imperfect. The theoretical perfect circle is the form of a circle, and existing circles all derive from that form. All objects—from tables to fish to rocks—derive from their corresponding forms. They can also derive from the forms of concepts—a beautiful table derives from the form of beauty, for example.
| Problems With Forms To better understand how the theory of the forms works, we can look at how Aristotle—another ancient Greek philosopher and Plato’s student—argued against it. Here are two of Aristotle’s most significant critiques of Plato’s idealized forms: 1) Forms can’t create objects. According to Plato, forms cause the existence of objects. But Aristotle argues that if forms are eternal and unchanging, they can’t cause anything—in fact, they can’t do anything at all. Any kind of activity or motion would require the forms to change in some way, even if it just meant briefly changing from “not currently creating something” to “currently creating something” and back. 2) The “third man” argument, which is as follows: John is a man. All men derive from the form of a man—a perfect, unique ideal of man-ness. We’ll call this form Frank. Since Frank is the perfect ideal of a man, he himself is naturally a man as well. But as previously stated, all men derive from the form of a man. So if Frank is a man, he must derive from some even more perfect ideal of man-ness—some third man that both John and Frank can derive from. This logic loop extends indefinitely. |
Highest Level: The Form of the Good and the Sun
Socrates argues that all forms—and the objects and images that derive from them—derive from the form of the good. Since the forms are perfect ideals, they must be good. You wouldn’t call a perfect circle a bad circle, for example.
Moreover, knowledge—the way we determine what is true and how we grasp reality—comes from an understanding of the forms. Therefore, the form of the good is the ultimate source of all knowledge and truth. Socrates compares the form of the good to the sun: Just as the sun provides the warmth for things to grow and the light for us to perceive them, the form of the good provides the reality for us to study and the truth for us to make sense of it.
(Shortform note: The form of the good and the sun strongly influenced early Christian theology and philosophy, with theologians connecting Plato’s theories to their understanding of God. For example, early Christian theologian Saint Augustine rejected the idea of a material, physical God after studying Platonic philosophy. Instead, he argued that God was an immaterial being responsible for creating the material world—much like how the form of the good is an immaterial concept that creates reality.)
Exercise/Discussion
Do you agree with Plato’s view that the search for philosophical knowledge is superior to worldly concerns like wealth and politics? Why or why not?

———End of Preview———
Like what you just read? Read the rest of the world's best book summary and analysis of Plato's "The Republic" at Shortform.
Here's what you'll find in our full The Republic summary:
- Plato’s concept of justice
- Why living a moral life is good for its own sake
- How later philosophers interpreted and responded to the ideas in The Republic






